Carbon Nanotubes

Figure 1 – Carbon nanotube

In this section we’ll talk about carbon nanotubes, their amazing properties,  procedure of producing carbon nanotubes and of course their application in nanosensors.

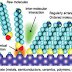
As we know the carbon nanotubes like nanowires are 1 D nanostructures. They are made from carbon and their diameter is just few nanometers while their distance is million times larger than diameter. Carbon nanotubes can be viewed like they are formed from graphene sheets forming closed cylinder. Since their length can be million times larger than their diameter it’s obvious to assume that they have some quantum effects and unique characteristics. Scientists proved that carbon nanotubes have unique stiffness, strength, and tenacity characteristics compared to other fiber materials. Thermal and electrical conductivity are also very high, and comparable to typical conductive materials.

The carbon nanotubes can be single walled shortly SWCNT or multi-walled carbon nanotubes MWCNT. Properties of CNTs have peaked the interest of many in researchers and industry, and are currently being considered for use in multiple fields of applications such as nanosensors, nanoelectronics etc.

As we mentioned before graphene sheet can be rolled up but it’s very important to know how they’re rolled up. The reason for that is because they can be rolled in different directions with respect to graphene lattice, and each organization results in a different atomic orientation of the CNT surface atoms. Each orientation has unique electrical, optical and chemical properties.

SWCNT are described as one-dimensional unit cell. We introduce two vectors a₁ and a₂ which are unit vectors defined by the dimensions and directionality of the unit cell. The mathematical expression of vectors a₁ and a₂ are given below: 

$$\begin{align} & {{a}_{1}}=a\left( \frac{\sqrt{3}}{2},\frac{1}{2} \right); \\ & {{a}_{2}}=a\left( \frac{\sqrt{3}}{2},-\frac{1}{2} \right) \\ \end{align}$$

In previous equations characteristic length a  signifies the C-C bond length and the related numbers indicate direction of the vector. Circumferential vector C_h is defined by a linear combination of the unit vectors a₁ and a₂ where n and m are integers: 

$${{C}_{h}}=m{{a}_{1}}+m{{a}_{2}}$$

The unit vector of the nanotube is defined in a similar way: 

$$T={{t}_{1}}{{a}_{1}}+{{t}_{2}}{{a}_{2}}$$

Direction in which the graphene sheet is wrapped is represented by a pair of indices. The integer’s n and m denote the number of unit vectors along two directions in the honeycomb crystal lattice of graphene.

The variation of CNTs are:

• If m = 0 nanotubes are called zigzag
• If m = n nanotubes are called chiral and
• Otherwise they are called chiral 

Figure 2 – Types of nanotubes

The radius of an ideal nanotube can be calculated from its (n,m) indices as follows: 

$$r=\frac{\left| C \right|}{2\pi }=\frac{\sqrt{3}}{2\pi }a\sqrt{{{n}^{2}}+{{m}^{2}}+nm}$$

Size of the circumferential vector C is the circumference of the nanotube, which is 2*π*r, which is similar to the circle. The size of vector C can be calculated with the characteristic length a and the integer n and m that define the vector C.